Diamo un'occhiata a una parte della matematica che si nasconde dietro il nostro StarTracker. Questo articolo riguarda in particolare il tipo a "triangolo isoscele".
Consideriamo lo schema seguente. Il nostro tracker ha due bracci:
Un braccio mobile che trasporta la fotocamera ( AC nel disegno ).
Un braccio fisso, fisso ( AB nel disegno ).
Il braccio mobile con la fotocamera è collegato al braccio fisso tramite una cerniera. Lo scopo è far ruotare il braccio della fotocamera attorno al braccio fisso esattamente alla stessa velocità con cui ruota la terra.
La velocità della rotazione terrestre
- La terra impiega 23 ore 56 minuti 4 secondi per ruotare attorno al suo asse.
- Espresso in minuti, è circa 23 × 60 + 56 = 1.436 minuti
- Una rotazione è uguale a 360 °
Implica la velocità di rotazione della terra: 360 ° / 1.436 minuti ~ 0,25 ° al minuto ~ 15 ° all'ora.
Neutralizzare la rotazione terrestre
L'obiettivo principale è ruotare il braccio della fotocamera alla velocità di 0,25 ° ogni minuto per neutralizzare l'effetto della rotazione terrestre, cioè, aumentare θ nel diagramma seguente al ritmo di 0,25 ° ogni minuto.
Meccanicamente ciò si ottiene aumentando la lunghezza "S" con l'aiuto di una vite collegata a un motore. Quando S aumenta, l'angolo θ aumenta di conseguenza. Aumentando la lunghezza S a una velocità calcolata precisa, l'angolo θ può essere aumentato a 0,25 ° al minuto che è il nostro obiettivo.
Vediamo come si arriva a questa velocità.
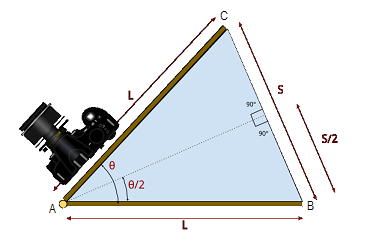
Sappiamo che θ deve aumentare a 0,25 ° al minuto e per aumentare θ, dobbiamo aumentare S. Calcoliamo quindi la relazione tra S e θ.
△ ABC è un triangolo isoscele. Questo perché entrambi i bracci AB e AC hanno la stessa lunghezza. Per semplificare i nostri calcoli, dividiamo △ ABC in due parti uguali separate dalla linea tratteggiata.
I due nuovi triangoli sono triangoli rettangoli. Applichiamo alcuni semplici calcoli trigonometrici :
sin ( θ / 2) = (S / 2) / L
sin ( θ / 2) = S / 2 x L
S = 2 x L x sin ( θ / 2)
Calcoliamo l'aumento richiesto di S ogni ora per il tracciamento. (calcolo approssimativo).
Supponiamo all'inizio S = 0 mm, θ = 0 ° ( in realtà l'angolo di inizio potrebbe essere maggiore per problemi meccanici nel parallelismo dei bracci ).
Dopo 1 ora, θ dovrebbe essere 15 ° (velocità di rotazione terrestre)
S = 2 x L x sin (θ / 2) all'ora
S = 2 x L x sin (15 / 2) all'ora
S = 2 x L x 0.1305 all'ora
S = 0.261 x L all'ora
Nota: la rotazione della Terra non è esattamente di 15 ° all'ora. Ricorda che la Terra impiega 23h 56m 4s per effettuare una rotazione e ciò si traduce in 15,04 ° all'ora.
Useremo questa velocità più accurata nel software che scriveremo in seguito.
Si veda ad esempio, se nel progetto avessimo scelto la lunghezza del braccio L = 300 mm, S = 78,3 mm alla fine di 1 ora di tracciamento.
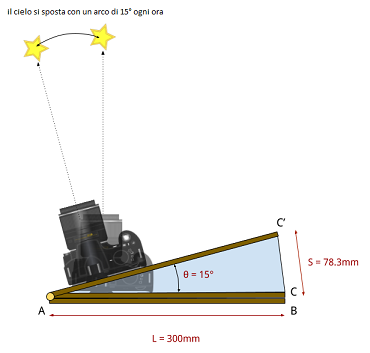
La geometria del nostro Tracker presenta un errore intrinseco che crea una deriva lenta durante il monitoraggio del cielo. Nel più elementare dei tracker questa deriva inizia a diventare evidente in circa 10 minuti. Nel nostro tracker "isoscele" descritto in questo sito Web, la deriva inizia a diventare evidente dopo 8 minuti.
Matematicamente la deriva o l'errore è dovuto alla relazione non lineare tra l'angolo incluso del triangolo e la lunghezza della base (spostamento dell'asta filettata / dado). Un aumento lineare (o costante della velocità) della lunghezza della base di un triangolo non produce un aumento lineare dell'angolo incluso.
Ciò è evidente dalla seguente formula :
S = 2 · L · sin (θ / 2)
'L' è la lunghezza dei due bracci
'θ' è l'angolo incluso dei bracci
'S' è la base o lo spostamento del dado / barra filettata.
⇒ θ = 2 · sin - 1 (S / (2 · L))
Quando risolviamo per dθ / dt (tasso di aumento se angolo) dato un dS / dt costante, otteniamo una soluzione non lineare. In termini più semplici, la velocità angolare del nostro tracker non sarà costante quando la barra filettata viene ruotata a una velocità costante.
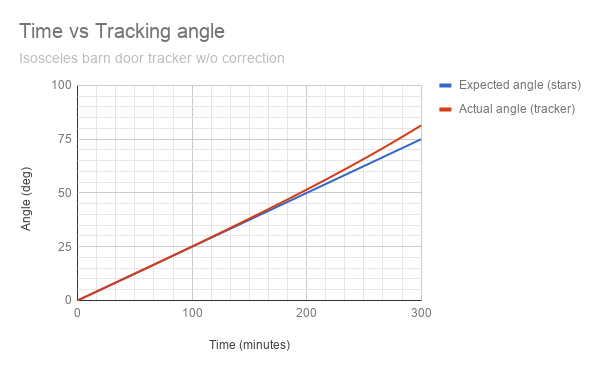
La seguente tabella mostra come l'angolo effettivo inizia a spostarsi dall'angolo previsto per un sistema a "triangolo isoscele" che non è compensato dall'errore tangente.
Questo esempio è per un supporto isoscele con una lunghezza del braccio di 300 mm.
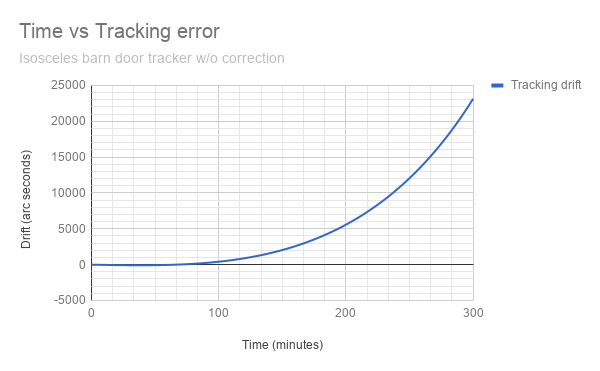
La seguente tabella mostra l'effettivo errore di deriva, quando il tracker non è compensato per l'errore tangente.
Questo esempio è per un supporto isoscele con una lunghezza del braccio di 300 mm.
Soluzioni tradizionali di tipo meccanico
Il modo tradizionale di risolvere questo problema è mediante miglioramenti meccanici. In genere un secondo braccio è stato introdotto sul lato della fotocamera. Con l'introduzione di un secondo braccio per guidare il braccio della videocamera, l'accuratezza del tracciamento è stata notevolmente aumentata e questo aumento della precisione consente tempi di esposizione fino a un'ora.
Un altro metodo tradizionale è l'introduzione di un profilo guida ( una camma sagomata ) appositamente progettato tra il braccio della telecamera e l'attuatore. Questo profilo genera una funzione negativa nell'avanzamento, annullando così l'errore di tracciamento.
Moderna soluzione "intelligente"
Le soluzioni tradizionali aumentarono sostanzialmente la difficoltà di fabbricazione del tracker, inoltre queste soluzioni risalgono a un'epoca in cui l'elettronica e i microcontrollori erano i giocattoli di ingegneri e tecnici specializzati e quindi fuori dalla portata degli appassionati. La risoluzione dell'errore tangente attraverso il software è attualmente la più semplice ed elegante.
L'errore tangente viene creato perché una velocità costante applicata sull'asta filettata del tracker produce una risposta non lineare nell'angolo del localizzatore.
La soluzione per questo problema è regolare continuamente la velocità applicata all'asta filettata in modo da mantenere una risposta lineare costante nell'angolo di apertura del tracker.
Ciò può essere ottenuto tramite software in esecuzione in un piccolo micro controller come Arduino. Questo concetto è visualizzato nella tabella seguente:
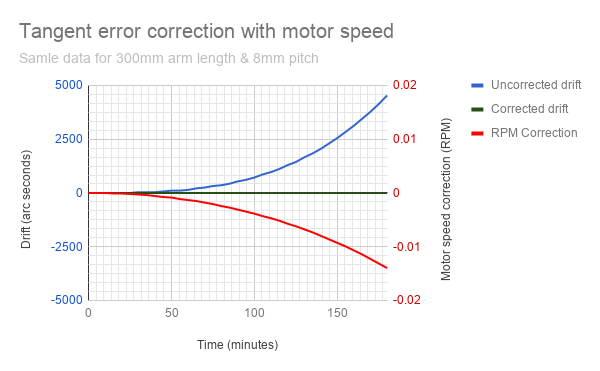
Il codice sorgente del software per eseguire questa correzione è fornito gratuitamente ed è open source: CORREZIONE ERRORE TANGENZIALE
Torna a ARDUINO →
